OPENING QUESTIONS: Let's start by sketching out what we know about circuits so far (this is our first step in developing a circuit model)
1) How does charge change through a circuit? (caps, resistors, series, parallel)
2) How does current change through a circuit? (caps, resistors, series, parallel)
3) How does voltage change through a circuit? (caps, resistors, series, parallel)
OBJECTIVE: I will develop a working model to calculate circuit values during today's class
════════════════════
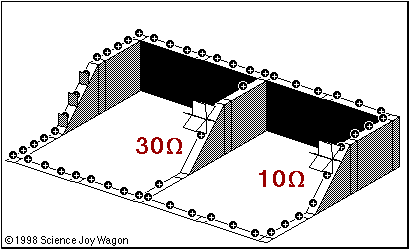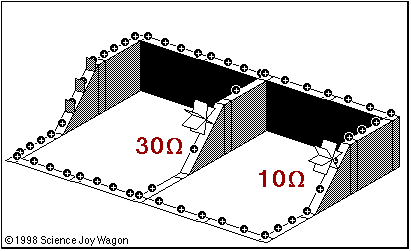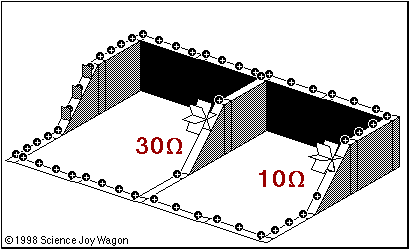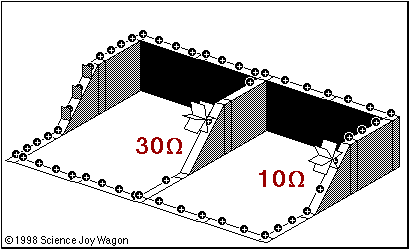
Take a look at this animation (note the march of POSITIVE charges... our convention in physics is that current flows from positive to negative):
1) Where is the battery located?
- How do you know?
2) Make a statement about current with regards to the 30 ohm and the 10 ohm resistors.
3) Make a statement about the height of the structure.... which circuit component is represented there?
4) What is the result of adding more resistors to the circuit?
5) How does the current immediately after the battery relate to the current just before it goes 'uphill'?
════════════════════
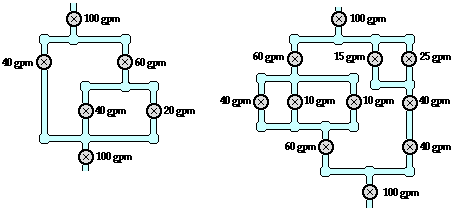
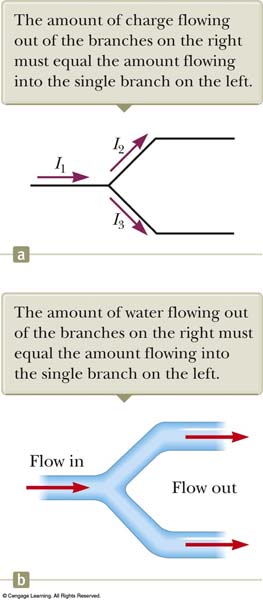
Notice that every time there is a branch in the pipe, the current is split....
The degree in which it is split is entirely dependant on the.... WHAT (it is not apparent in this diagram)
════════════════════
Essentials Summary:
- The sum of the voltage in an electric circuit MUST be zero:
- Initial electric potential minus each voltage drop across each element = 0
- remember the initial animation
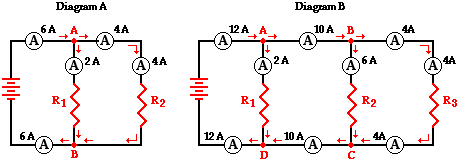
2. Any time the circuit branches the current flow into the branch MUST equal the current flowing out of the branch
════════════════════
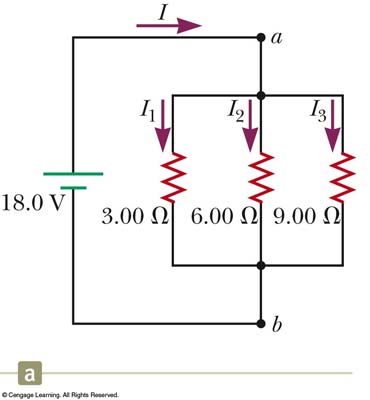
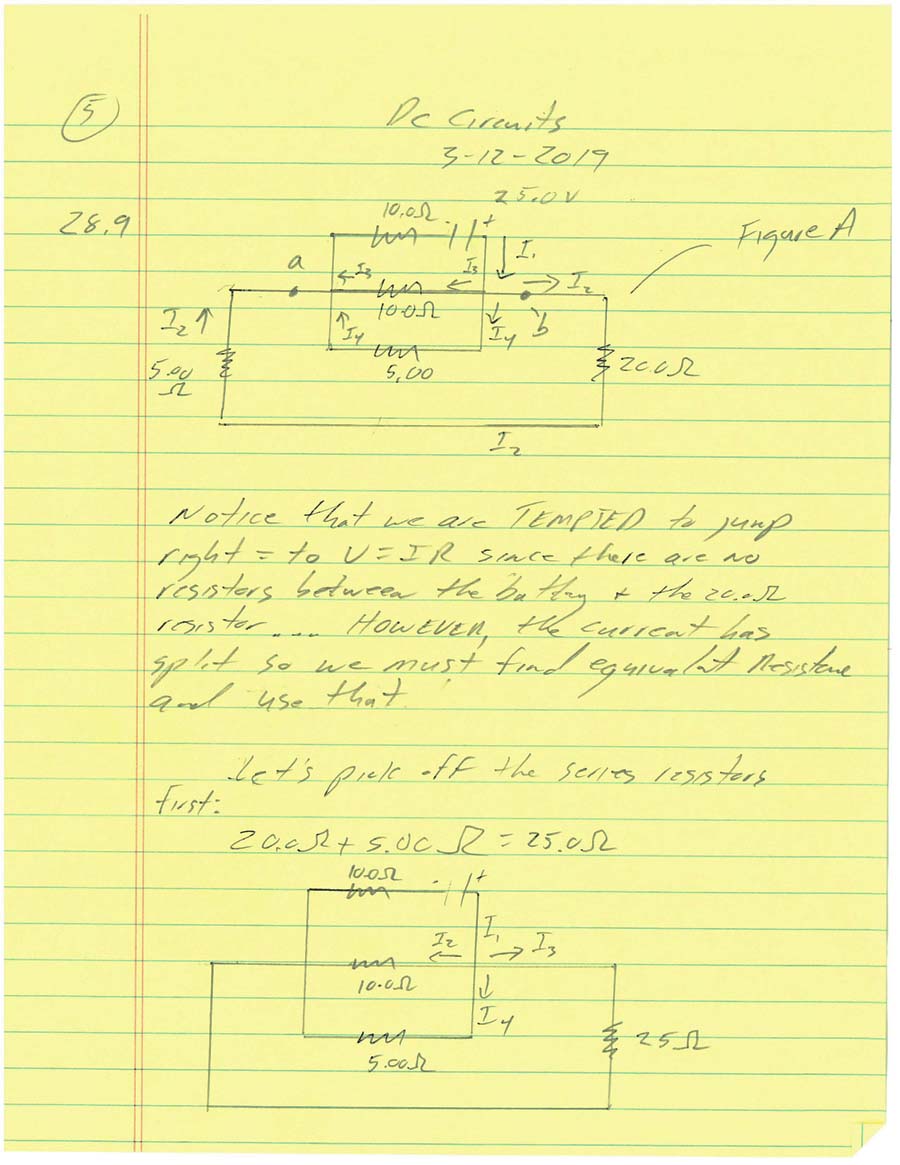
Consider the following circuit:
Find the voltage and current at points a and b:
For point a)
1) To find the voltage at point a:
a) We gotta find the current first so let's do that:
b) V = IR, so I = V/R so let's find the equivalent resistance first:
- 1/R1 + 1/R2 + 1/R3 = 1/R sooooooo
- 1/3Ω + 1/6Ω + 1/9Ω = 1.64 Ω
- V/R = I so 18V/1.64Ω = 10.98 A = 11Amps (s.f.)
c) no resistors are present before point a, so the voltage at point a is just the given voltage: 18V
d) We can (and should) use the equivalent resistance to find the total drop in the electric potential across those 3 resistors in parallel:
- V = IR = (10.98A)(1.64Ω) = 18 V which is as expected
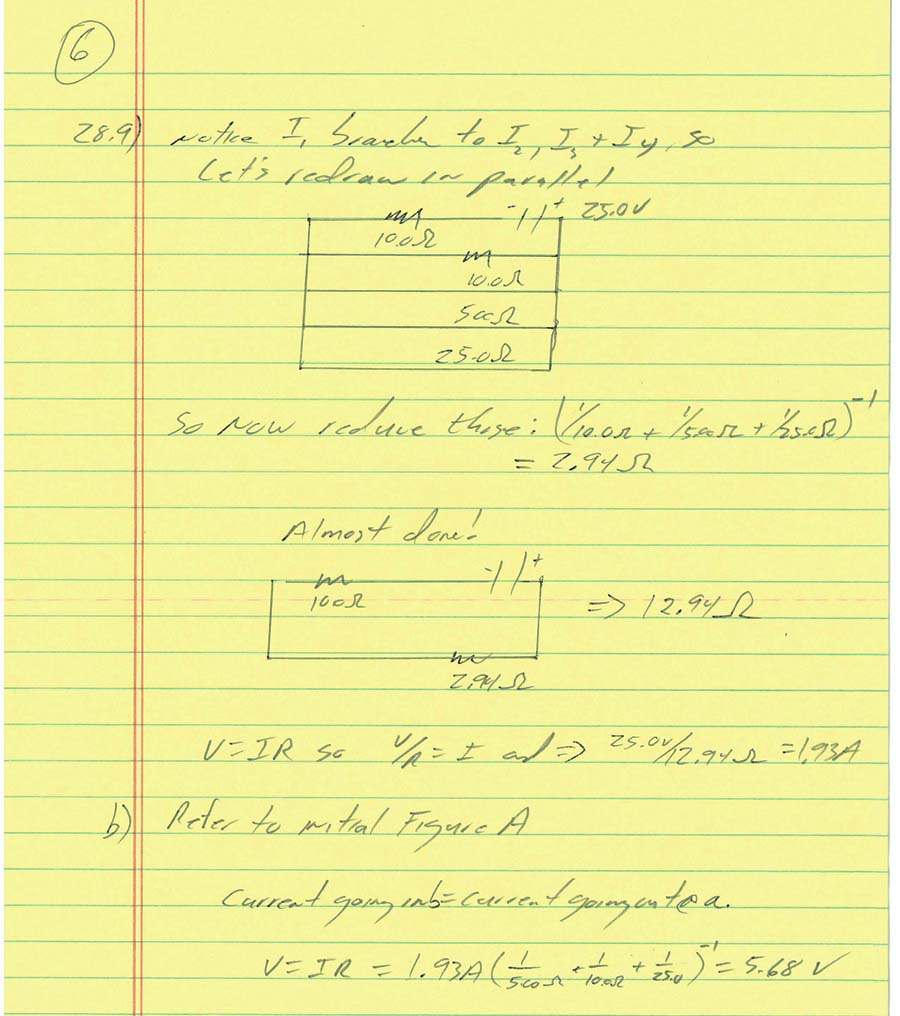
- That means, however that the drop in electric potential across EACH resistor in parallel is 18 V
2) What is the current through each resistor?
- We know the current changes because it has to "branch" into each of the 3 resistors
- We know the voltage drop across each of those resistors is constant at 18 Volts...
- We can, therefore, find the current in each branch...let's do that:
- I1 = V/R1 = (18V)/(3Ω) = 6Amps
- I2 = V/R2 = (18V)/(6Ω) = 3Amps
- I3 = V/R3 = (18V)/(9Ω) = 2 Amps
- If we add up all that current we get right back to 11 Amps... which we expect....
- SOOOO what about the voltage "drop" across each resistor in parallel.......? (It is 18 V each!)
- Find the equivalent resistance for the circuit
- How much current is flowing through the circuit?
- Find the voltage drop over each resistor
- Make a qualitative statement about the amount of current flowing through each resistor
- Make adustments to your model
════════════════════
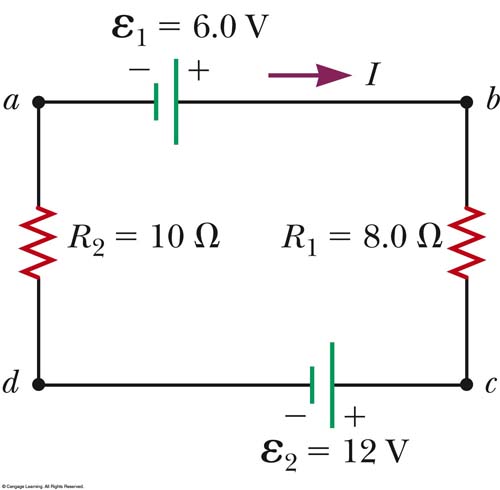
Now take a look at the circuit below:
- What do you notice that is different from our previous examples?
- What do you notice about the voltages? (Our convention is that voltage drops when we go left to right and adds when we go right to left)
- Calculate the current
- Compare your results with example 28.6
════════════════════
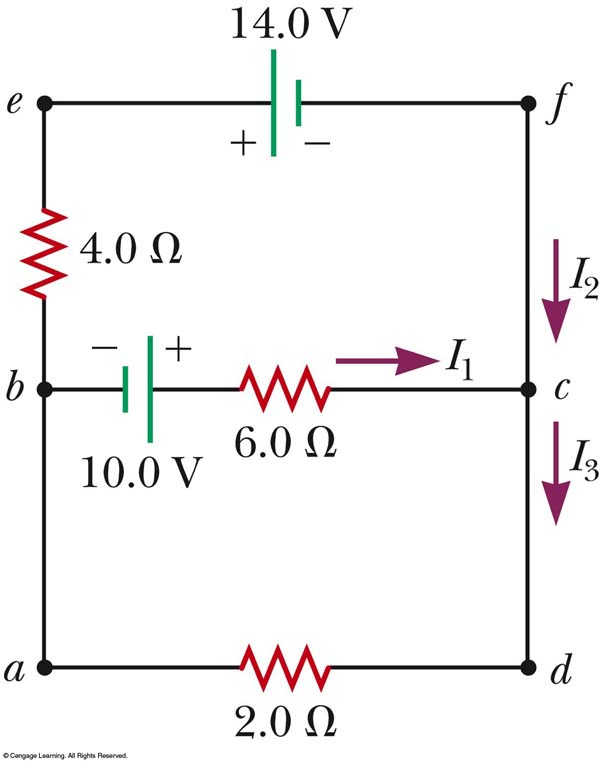
Now take a look at this one... why is that we CANNOT write an equivalent resistance for the 6.0 ohm and 2.00 ohm resistors?
HOMEWORK:
1) Please review AND annotate your homework (notes are above)
2) Each problem is trying to teach you something different... find out what that is and comment on that.
Problem #5, 9, 17
We'll work on writing equivalent circuit diagrams tomorrow so please take a gander at
ANNOTATED ANSWERS:






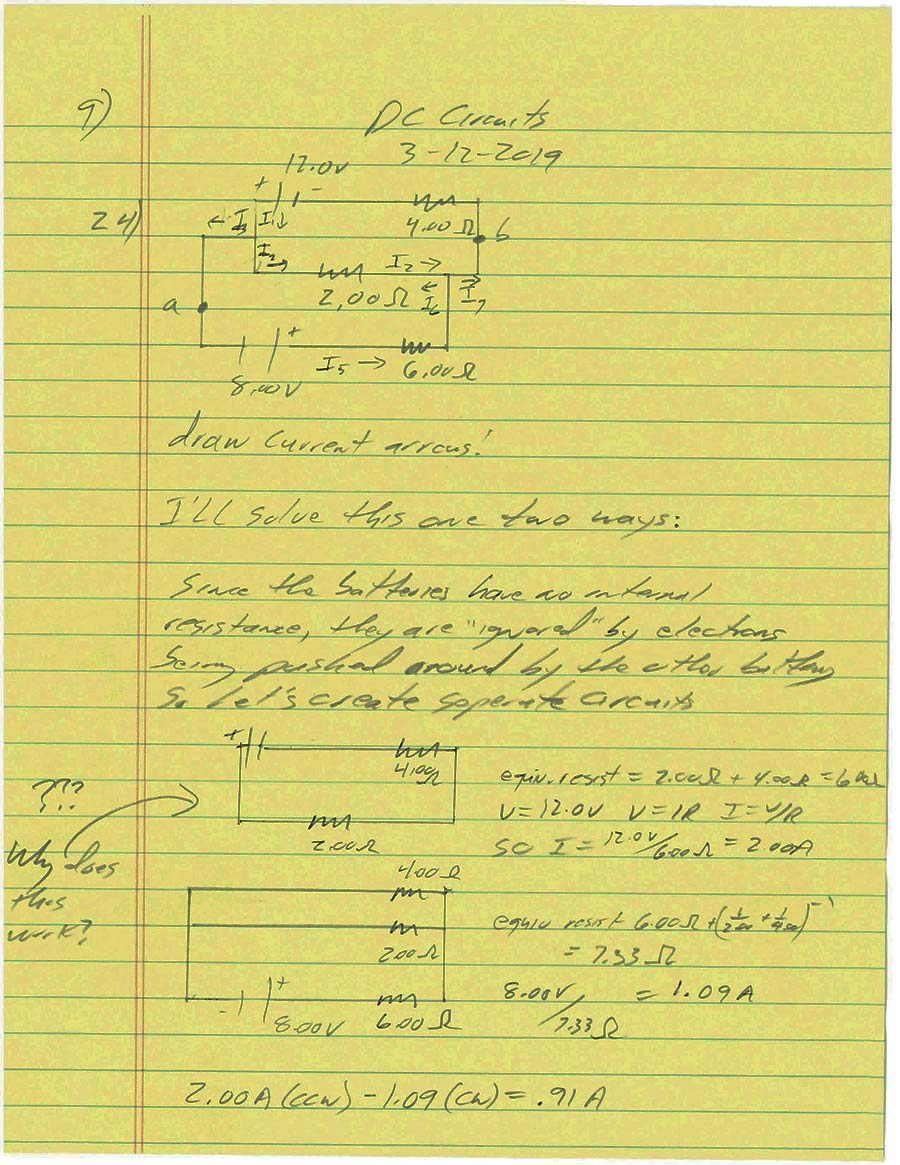
════════════════════
Hold off on these for now:
Adding a second battery can be nasty... take a look at THIS for help
24, 26